授業内容

１章　組み合わせ回路（教科書p.17-) 1.3　より簡単な回路を設計するために−カルノー図− 1.3.1　簡単化のいろいろな方法 1.3.2　カルノー図とは

２つの論理変数B,Aの真理値表は B A Z 0 0 0 0 1 1 1 0 0 1 1 1 となり，この表で加法標準形設計方による論理式は，Z=¬BA＋BAとなる． この真理値表を２つの論理変数B，Aによるカルノー図で表すと B＼A 0 1 0 0 １ 1 0 １ と書ける． この論理変数B，Aについての関係を以下のベン図に表現する．

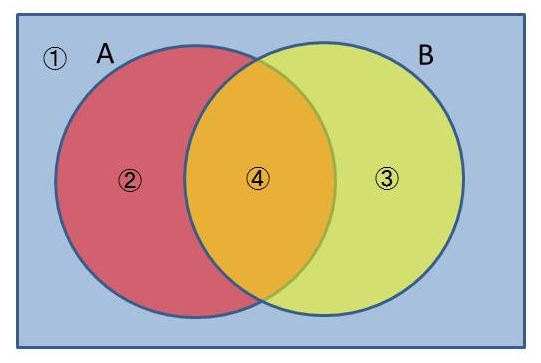
論理変数B,Aのベン図

このベン図の領域�@から�Cは，それぞれに �@は，¬B¬A，�Aは，¬BA，�Bは，B¬A，�Cは，BAを表している．（¬は否定を表す） このベン図上の�@から�Cをカルノー図内の部屋に当てはめると B＼A 0 1 0 �@ �A 1 �B �C となる． 先ほどの真理値表では，�Aと�Cに１があるので，論理式はZ=¬BA＋BAであった． 論理式で共通する論理変数Aで式をまとめて簡単化するとZ=A（¬B＋B）=A・１=Aとなる． ベン図上だと上記の式は，Aは，赤い円，¬B＋Bは，長方形枠を表しており， 赤い円と長方形枠のANDをとるわけだから，結果的に赤い円，すなわちAとなることを示している．． つまり，Z=�A＋�Cということだから，ベン図のAの円と�A＋�Cが一致しているのがわかる．

宿題１０

以下のカルノー図�@から�Dの簡単化前Zと後の論路式Z’を答えなさい．

例 DC＼BA 00 01 11 10 00 01 １ １ 11 10 １ １ （¬は否定を表す） 簡単化前の論理式　Z=¬DC¬BA＋¬DCBA+D¬C¬B¬A+DCBA＋D¬CB¬A 簡単化後の論理式　Z'＝¬DCA＋D¬C¬A

�@ DC＼BA 00 01 11 10 00 １ 01 １ 11 １ 10 １ �A DC＼BA 00 01 11 10 00 １ １ 01 １ 11 １ 10 １ １ �B DC＼BA 00 01 11 10 00 １ １ 01 １ １ １ １ 11 １ １ 10 １ １ �C DC＼BA 00 01 11 10 00 １ １ 01 １ １ 11 １ １ 10 １ １ �D DC＼BA 00 01 11 10 00 １ １ １ １ 01 １ １ １ １ 11 １ １ １ １ 10 １ １ １ １

提出期限

7/6（月）17：00　A４レポート用紙に表紙は不要で１枚目の上部に出席番号と名前を明記し， 松尾のメールボックスまで

連絡事項

• 次回は教室です．
• A4グラフ用紙を準備しておくこと

レポート

なし